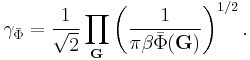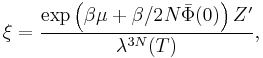Polymer field theory
A polymer field theory is a statistical field theory describing the statistical behavior of a neutral or charged polymer system. It can be derived by transforming the partition function from its standard many-dimensional integral representation over the particle degrees of freedom in a functional integral representation over an auxiliary field function, using either the Hubbard-Stratonovich transformation or the delta-functional transformation. Computer simulations based on polymer field theories have been shown to deliver useful results, for example to calculate the structures and properties of polymer solutions (Baeurle 2007, Schmid 1998), polymer melts (Schmid 1998, Matsen 2002, Fredrickson 2002) and thermoplastics (Baeurle 2006).
Contents |
Canonical ensemble
Particle representation of the canonical partition function
The standard continuum model of flexible polymers, introduced by Edwards (Edwards 1965), treats a solution composed of  linear monodisperse homopolymers as a system of coarse-grained polymers, in which the statistical mechanics of the chains is described by the continuous Gaussian thread model (Baeurle 2007) and the solvent is taken into account implicitly. The Gaussian thread model can be considered as the continuum limit of the discrete Gaussian chain model, in which the polymers are described as continuous, linearly elastic filaments. The canonical partition function of such a system, kept at an inverse temperature
linear monodisperse homopolymers as a system of coarse-grained polymers, in which the statistical mechanics of the chains is described by the continuous Gaussian thread model (Baeurle 2007) and the solvent is taken into account implicitly. The Gaussian thread model can be considered as the continuum limit of the discrete Gaussian chain model, in which the polymers are described as continuous, linearly elastic filaments. The canonical partition function of such a system, kept at an inverse temperature 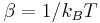 and confined in a volume
and confined in a volume  , can be expressed as
, can be expressed as
where ![\bar{\Phi} \left[ \mathbf{r} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/14169d6dc8b836fa14b07a4ee8e19d19.png) is the potential of mean force given by,
is the potential of mean force given by,
representing the solvent-mediated non-bonded interactions among the segments, while ![\Phi_0 [\mathbf{r}]](/2012-wikipedia_en_all_nopic_01_2012/I/e36aaba599a937420445a1e00d8ebb25.png) represents the harmonic binding energy of the chains. The latter energy contribution can be formulated as
represents the harmonic binding energy of the chains. The latter energy contribution can be formulated as
where  is the statistical segment length and
is the statistical segment length and  the polymerization index.
the polymerization index.
Field-theoretic transformation
To derive the basic field-theoretic representation of the canonical partition function, one introduces in the following the segment density operator of the polymer system
Using this definition, one can rewrite Eq. (2) as
Next, one converts the model into a field theory by making use of the Hubbard-Stratonovich transformation or delta-functional transformation
where ![F \left[ \hat{\rho} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/03e93be789873f051a3e5ea799102d32.png) is a functional and
is a functional and ![\delta \left[ \rho - \hat{\rho} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/385f6fcdf1ce973ea601a060c1a8f5a4.png) is the delta functional given by
is the delta functional given by
with ![w (\mathbf{r}) = \sum\nolimits_{\mathbf{G}} w (\mathbf{G})\exp \left[ i \mathbf{G} \mathbf{r} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/de7dd80ffc94c967ab47e785b5dc79ed.png) representing the auxiliary field function. Here we note that, expanding the field function in a Fourier series, implies that periodic boundary conditions are applied in all directions and that the
representing the auxiliary field function. Here we note that, expanding the field function in a Fourier series, implies that periodic boundary conditions are applied in all directions and that the 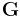 -vectors designate the reciprocal lattice vectors of the supercell.
-vectors designate the reciprocal lattice vectors of the supercell.
Basic field-theoretic representation of canonical partition function
Using the Eqs. (3), (4) and (5), we can recast the canonical partition function in Eq. (1) in field-theoretic representation, which leads to
where
can be interpreted as the partition function for an ideal gas of non-interacting polymers and
is the path integral of a free polymer in a zero field with elastic energy
In the latter equation the unperturbed radius of gyration of a chain 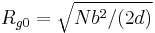 , where the space dimension
, where the space dimension 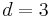 . Moreover, in Eq. (6) the partition function of a single polymer, subjected to the field
. Moreover, in Eq. (6) the partition function of a single polymer, subjected to the field 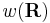 , is given by
, is given by
Grand canonical ensemble
Basic field-theoretic representation of grand canonical partition function
To derive the grand canonical partition function, we use its standard thermodynamic relation to the canonical partition function, given by
where  is the chemical potential and
is the chemical potential and 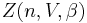 is given by Eq. (6). Performing the sum, this provides the field-theoretic representation of the grand canonical partition function,
is given by Eq. (6). Performing the sum, this provides the field-theoretic representation of the grand canonical partition function,
where
is the grand canonical action with ![Q [ i w ]](/2012-wikipedia_en_all_nopic_01_2012/I/a01c17f89317a936f8cd71fd11a4a1de.png) defined by Eq. (8) and the constant
defined by Eq. (8) and the constant
Moreover, the parameter related to the chemical potential is given by
where 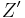 is provided by Eq. (7).
is provided by Eq. (7).
Mean field approximation
A standard approximation strategy for polymer field theories is the mean field (MF) approximation, which consists in replacing the many-body interaction term in the action by a term where all bodies of the system interact with an average effective field. This approach reduces any multi-body problem into an effective one-body problem by assuming that the partition function integral of the model is dominated by a single field configuration. A major benefit of solving problems with the MF approximation, or its numerical implementation commonly referred to as the self-consistent field theory (SCFT), is that it often provides some useful insights into the properties and behavior of complex many-body systems at relatively low computational cost. Successful applications of this approximation strategy can be found for various systems of polymers and complex fluids, like e.g. strongly segregated block copolymers of high molecular weight, highly concentrated neutral polymer solutions or highly concentrated block polyelectrolyte (PE) solutions (Schmid 1998, Matsen 2002, Fredrickson 2002). There are, however, a multitude of cases for which SCFT provides inaccurate or even qualitatively incorrect results (Baeurle 2006a). These comprise neutral polymer or polyelectrolyte solutions in dilute and semidilute concentration regimes, block copolymers near their order-disorder transition, polymer blends near their phase transitions, etc. In such situations the partition function integral defining the field-theoretic model is not entirely dominated by a single MF configuration and field configurations far from it can make important contributions, which require the use of more sophisticated calculation techniques beyond the MF level of approximation.
Higher-order corrections
One possibility to face the problem is to calculate higher-order corrections to the MF approximation. Tsonchev et al. developed such a strategy including leading (one-loop) order fluctuation corrections, which allowed to gain new insights into the physics of confined PE solutions (Tsonchev 1999). However, in situations where the MF approximation is bad many computationally demanding higher-order corrections to the integral are necessary to get the desired accuracy.
Renormalization techniques
An alternative theoretical tool to cope with strong fluctuations problems occurring in field theories has been provided in the late 1940s by the concept of renormalization, which has originally been devised to calculate functional integrals arising in quantum field theories (QFT's). In QFT's a standard approximation strategy is to expand the functional integrals in a power series in the coupling constant using perturbation theory. Unfortunately, generally most of the expansion terms turn out to be infinite, rendering such calculations impracticable (Shirkov 2001). A way to remove the infinities from QFT's is to make use of the concept of renormalization (Baeurle 2007). It mainly consists in replacing the bare values of the coupling parameters, like e.g. electric charges or masses, by renormalized coupling parameters and requiring that the physical quantities do not change under this transformation, thereby leading to finite terms in the perturbation expansion. A simple physical picture of the procedure of renormalization can be drawn from the example of a classical electrical charge,  , inserted into a polarizable medium, such as in an electrolyte solution. At a distance
, inserted into a polarizable medium, such as in an electrolyte solution. At a distance  from the charge due to polarization of the medium, its Coulomb field will effectively depend on a function
from the charge due to polarization of the medium, its Coulomb field will effectively depend on a function 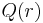 , i.e. the effective (renormalized) charge, instead of the bare electrical charge,
, i.e. the effective (renormalized) charge, instead of the bare electrical charge,  . At the beginning of the 1970s, K.G. Wilson further pioneered the power of renormalization concepts by developing the formalism of renormalization group (RG) theory, to investigate critical phenomena of statistical systems (Wilson 1971).
. At the beginning of the 1970s, K.G. Wilson further pioneered the power of renormalization concepts by developing the formalism of renormalization group (RG) theory, to investigate critical phenomena of statistical systems (Wilson 1971).
Renormalization group theory
The RG theory makes use of a series of RG transformations, each of which consists of a coarse-graining step followed by a change of scale (Wilson 1974). In case of statistical-mechanical problems the steps are implemented by successively eliminating and rescaling the degrees of freedom in the partition sum or integral that defines the model under consideration. De Gennes used this strategy to establish an analogy between the behavior of the zero-component classical vector model of ferromagnetism near the phase transition and a self-avoiding random walk of a polymer chain of infinite length on a lattice, to calculate the polymer excluded volume exponents (de Gennes 1972). Adapting this concept to field-theoretic functional integrals, implies to study in a systematic way how a field theory model changes while eliminating and rescaling a certain number of degrees of freedom from the partition function integral (Wilson 1974).
Hartree renormalization
An alternative approach is known as the Hartree approximation or self-consistent one-loop approximation (Amit 1984). It takes advantage of Gaussian fluctuation corrections to the 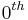 -order MF contribution, to renormalize the model parameters and extract in a self-consistent way the dominant length scale of the concentration fluctuations in critical concentration regimes.
-order MF contribution, to renormalize the model parameters and extract in a self-consistent way the dominant length scale of the concentration fluctuations in critical concentration regimes.
Tadpole renormalization
In a more recent work Efimov and Nogovitsin showed that an alternative renormalization technique originating from QFT, based on the concept of tadpole renormalization, can be a very effective approach for computing functional integrals arising in statistical mechanics of classical many-particle systems (Efimov 1996). They demonstrated that the main contributions to classical partition function integrals are provided by low-order tadpole-type Feynman diagrams, which account for divergent contributions due to particle self-interaction. The renormalization procedure performed in this approach effects on the self-interaction contribution of a charge (like e.g. an electron or an ion), resulting from the static polarization induced in the vacuum due to the presence of that charge (Baeurle 2007). As evidenced by Efimov and Ganbold in an earlier work (Efimov 1991), the procedure of tadpole renormalization can be employed very effectively to remove the divergences from the action of the basic field-theoretic representation of the partition function and leads to an alternative functional integral representation, called the Gaussian equivalent representation (GER). They showed that the procedure provides functional integrals with significantly ameliorated convergence properties for analytical perturbation calculations. In subsequent works Baeurle et al. developed effective low-cost approximation methods based on the tadpole renormalization procedure, which have shown to deliver useful results for prototypical polymer and PE solutions (Baeurle 2006a, Baeurle 2006b, Baeurle 2007a).
Numerical simulation
Another possibility is to use Monte Carlo (MC) algorithms and to sample the full partition function integral in field-theoretic formulation. The resulting procedure is then called a polymer field-theoretic simulation. In a recent work, however, Baeurle demonstrated that MC sampling in conjunction with the basic field-theoretic representation is impracticable due to the so-called numerical sign problem (Baeurle 2002). The difficulty is related to the complex and oscillatory nature of the resulting distribution function, which causes a bad statistical convergence of the ensemble averages of the desired thermodynamic and structural quantities. In such cases special analytical and numerical techniques are necessary to accelerate the statistical convergence (Baeurle 2003, Baeurle 2003a, Baeurle 2004).
Mean field representation
To make the methodology amenable for computation, Baeurle proposed to shift the contour of integration of the partition function integral through thehomogeneous MF solution using Cauchy's integral theorem, providing its so-called mean-field representation. This strategy was previously successfully employed by Baer et al. in field-theoretic electronic structure calculations (Baer 1998). Baeurle could demonstrate that this technique provides a significant acceleration of the statistical convergence of the ensemble averages in the MC sampling procedure (Baeurle 2002, Baeurle 2002a).
Gaussian equivalent representation
In subsequent works Baeurle et al. (Baeurle 2002, Baeurle 2002a, Baeurle 2003, Baeurle 2003a, Baeurle 2004) applied the concept of tadpole renormalization, leading to the Gaussian equivalent representationof the partition function integral, in conjunction with advanced MC techniques in the grand canonical ensemble. They could convincingly demonstrate that this strategy provides a further boost in the statistical convergence of the desired ensemble averages (Baeurle 2002).
References
- Baeurle, S.A.; Nogovitsin, E.A. (2007). "Challenging scaling laws of flexible polyelectrolyte solutions with effective renormalization concepts". Polymer 48 (16): 4883. doi:10.1016/j.polymer.2007.05.080.
- Schmid, F. (1998). "Self-consistent-field theories for complex fluids". J. Phys.: Condens. Matter 10 (37): 8105. doi:10.1088/0953-8984/10/37/002.
- Matsen, M.W. (2002). "The standard Gaussian model for block copolymer melts". J. Phys.: Condens. Matter 14 (2): R21. doi:10.1088/0953-8984/14/2/201.
- Fredrickson, G.H.; Ganesan, V.; Drolet, F. (2002). "Field-Theoretic Computer Simulation Methods for Polymers and Complex Fluids". Macromolecules 35: 16. Bibcode 2002MaMol..35...16F. doi:10.1021/ma011515t.
- Baeurle, S.A.; Usami, T.; Gusev, A.A. (2006). "A new multiscale modeling approach for the prediction of mechanical properties of polymer-based nanomaterials". Polymer 47 (26): 8604. doi:10.1016/j.polymer.2006.10.017.
- Edwards, S.F. (1965). "The statistical mechanics of polymers with excluded volume". Proc. Phys. Soc. 85 (4): 613. doi:10.1088/0370-1328/85/4/301.
- Baeurle, S.A.; Efimov, G.V.; Nogovitsin, E.A. (2006a). "Calculating field theories beyond the mean-field level". Europhys. Lett. 75 (3): 378. doi:10.1209/epl/i2006-10133-6.
- Tsonchev, S.; Coalson, R.D.; Duncan, A. (1999). "Statistical mechanics of charged polymers in electrolyte solutions: A lattice field theory approach". Phys. Rev. E 60 (4): 4257. doi:10.1103/PhysRevE.60.4257.
- Shirkov, D.V. (2001). "Fifty years of the renormalization group". CERN Courier 41: 14. http://cerncourier.com/cws/article/cern/28487.
- Wilson, K.G. (1971). "Renormalization Group and Critical Phenomena. II. Phase-Space Cell Analysis of Critical Behavior". Phys. Rev. B 4 (9): 3184. doi:10.1103/PhysRevB.4.3184.
- Wilson, K.G.; Kogut J. (1974). "The renormalization group and the ε expansion". Phys. Rep. C 12 (2): 75. doi:10.1016/0370-1573(74)90023-4.
- de Gennes, P.G. (1972). "Exponents for the excluded volume problem as derived by the Wilson method". Phys. Lett. 38 A: 339.
- Amit, D.J. (1984). "Field theory, the renormalization group, and critical phenomena". Singapore, World Scientific. ASIN 9812561196. http://www.amazon.com/gp/reader/9812561196/ref=sib_dp_pt#reader-link.
- Efimov, G.V.; Nogovitsin, E.A. (1996). "The partition functions of classical systems in the Gaussian equivalent representation of functional integrals". Physica A 234: 506. doi:10.1016/S0378-4371(96)00279-8.
- Efimov, G.V.; Ganbold, G. (1991). "Functional Integrals in the Strong Coupling Regime and the Polaron Self-Energy". Phys. Stat. Sol. 168: 165. doi:10.1002/pssb.2221680116.
- Baeurle, S.A.; Efimov, G.V.; Nogovitsin, E.A. (2006b). "On a new self-consistent-field theory for the canonical ensemble". J. Chem. Phys. 124 (22): 224110. doi:10.1063/1.2204913. PMID 16784266.
- Baeurle, S.A.; Charlot, M.; Nogovitsin E.A. (2007a). "Grand canonical investigations of prototypical polyelectrolyte models beyond the mean field level of approximation". Phys. Rev. E 75: 011804. doi:10.1103/PhysRevE.75.011804.
- Baeurle, S.A. (2002). "Method of Gaussian Equivalent Representation: A New Technique for Reducing the Sign Problem of Functional Integral Methods". Phys. Rev. Lett. 89 (8): 080602. Bibcode 2002PhRvL..89h0602B. doi:10.1103/PhysRevLett.89.080602. PMID 12190451.
- Baeurle, S.A. (2003). "Computation within the auxiliary field approach". J. Comput. Phys. 184 (2): 540. Bibcode 2003JCoPh.184..540B. doi:10.1016/S0021-9991(02)00036-0.
- Baeurle, S.A. (2003a). "The stationary phase auxiliary field Monte Carlo method: a new strategy for reducing the sign problem of auxiliary field methodologies". Comput. Phys. Commun. 154 (2): 111. Bibcode 2003CoPhC.154..111B. doi:10.1016/S0010-4655(03)00284-4.
- Baeurle, S.A. (2004). "Grand canonical auxiliary field Monte Carlo: a new technique for simulating open systems at high density". Comput. Phys. Commun. 157 (3): 201. Bibcode 2004CoPhC.157..201B. doi:10.1016/j.comphy.2003.11.001.
- Baer, R.; Head-Gordon, M.; Neuhauser, D. (1998). "Shifted-contour auxiliary field Monte Carlo for ab initio electronic structure: Straddling the sign problem". J. Chem. Phys. 109 (15): 6219. Bibcode 1998JChPh.109.6219B. doi:10.1063/1.477300.
- Baeurle, S.A.; Martonak, R.; Parrinello, M. (2002a). "A field-theoretical approach to simulation in the classical canonical and grand canonical ensemble". J. Chem. Phys. 117 (7): 3027. Bibcode 2002JChPh.117.3027B. doi:10.1063/1.1488587.
![Z (n,V,\beta) = \frac{1}{n! (\lambda_T^3)^{n N}} \prod_{j=1}^n
\int D \mathbf{r}_j \exp \left( - \beta \Phi_0 \left[ \mathbf{r} \right]
- \beta \bar{\Phi} \left[ \mathbf{r} \right] \right), \qquad (1)](/2012-wikipedia_en_all_nopic_01_2012/I/9a2425e0f0f511b16a767ef9831a3612.png)
![\bar{\Phi} \left[ \mathbf{r} \right] = \frac{N^2}{2} \sum_{j=1}^n
\sum_{k=1}^n \int_0^1 ds \int_0^1 ds' \bar{\Phi}
\left( \left| \mathbf{r}_j (s) - \mathbf{r}_k (s') \right| \right)
- \frac{1}{2} n N \bar{\Phi} (0), \qquad (2)](/2012-wikipedia_en_all_nopic_01_2012/I/9fdf984605d6cc36d98648dd9ee6ad2a.png)
![\Phi_0 [\mathbf{r}] = \frac{3 k_B T}{2 N b^2} \sum_{l=1}^n \int_0^1 ds
\left| \frac{d \mathbf{r}_{l} (s)}{d s} \right|^2,](/2012-wikipedia_en_all_nopic_01_2012/I/1d55c947df1dfb6b6e632dcf873478a5.png)
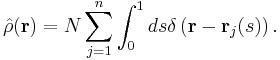
![\bar{\Phi} \left[ \mathbf{r} \right] = \frac{1}{2} \int d \mathbf{r}
\int d \mathbf{r}' \hat{\rho} (\mathbf{r}) \bar{\Phi}
( \left| \mathbf{r} - \mathbf{r}' \right| ) \hat{\rho}
(\mathbf{r}') - \frac{1}{2} n N \bar{\Phi} (0). \qquad (3)](/2012-wikipedia_en_all_nopic_01_2012/I/6442c40d8de9df448185e35f879f8989.png)
![\int D \rho \; \delta \left[ \rho - \hat{\rho} \right] F
\left[ \rho \right] = F \left[ \hat{\rho} \right], \qquad (4)](/2012-wikipedia_en_all_nopic_01_2012/I/b68c3c96659c616531fef1daed962327.png)
![\delta \left[ \rho - \hat{\rho} \right] = \int D w
e^{i \int d \mathbf{r} w (\mathbf{r}) \left[ \rho (\mathbf{r})
- \hat{\rho} (\mathbf{r}) \right] }, \qquad (5)](/2012-wikipedia_en_all_nopic_01_2012/I/347ad0153a266b2e5bb65cabce0f1373.png)
![Z (n,V,\beta) = Z_0
\int D w \exp \left[ - \frac{1}{2 \beta V^2} \int d \mathbf{r}
d \mathbf{r}' w (\mathbf{r}) \bar{\Phi}^{-1} (\mathbf{r}-\mathbf{r}')
w (\mathbf{r}') \right] Q^n [ i w ], \qquad (6)](/2012-wikipedia_en_all_nopic_01_2012/I/9a80769dfc20f787c335defbc85f9602.png)
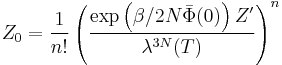
![Z' = \int D \mathbf{R} \exp \left[ - \beta U_0 (\mathbf{R}) \right] \qquad (7)](/2012-wikipedia_en_all_nopic_01_2012/I/59b4b237b8da153bf0f38a642b87c121.png)
![U_0 [\mathbf{R}] = \frac{k_B T}{4 R_{g0}^2} \int_0^1 ds
\left| \frac{d \mathbf{R} (s)}{d s} \right|^2.](/2012-wikipedia_en_all_nopic_01_2012/I/75d596c65e1a8bf5f5bfac2f37524a33.png)
![Q [ i w ] = \frac{\int D \mathbf{R} \exp \left[ - \beta U_0 [\mathbf{R}]
- i N \int_0^1 d s \; w (\mathbf{R} (s)) \right]}{\int D \mathbf{R}
\exp \left[ - \beta U_0 [\mathbf{R}] \right]}. \qquad (8)](/2012-wikipedia_en_all_nopic_01_2012/I/bc534ffcd8f67aed2cc43b694771e85c.png)
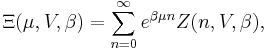
![\Xi(\xi,V,\beta) = \gamma_{\bar{\Phi}} \int D w
\exp \left[ - S [ w ] \right],](/2012-wikipedia_en_all_nopic_01_2012/I/3c936655e1f6ff01e97ac7417ad7f805.png)
![S [ w ] = \frac{1}{2 \beta V^2} \int d \mathbf{r} d \mathbf{r}'
w (\mathbf{r}) \bar{\Phi}^{-1} (\mathbf{r}-\mathbf{r}') w (\mathbf{r}') -
\xi Q [ i w ]](/2012-wikipedia_en_all_nopic_01_2012/I/aec72776833f8a3be45c902c105d409b.png)